スポンサーリンク
問題
連続する３個の整数A、B、Cがこの順で、３の倍数、５の倍数、７の倍数になっています。このようなA、B、Cで、Aが３桁の整数となるのは何通りか。
- 5通り
- 6通り
- 7通り
- 8通り
- 9通り
想定問題
解答と解説
解答
５
解説
ある数が3の倍数か否か、５の倍数か否かについては、どちらもすぐに判定できるので、７の倍数から確定させます。
（７の倍数－１）が5の倍数になるためには、７の倍数の１の位が１か６です。
そのような７の倍数と、その手前の数２つを書きだします。
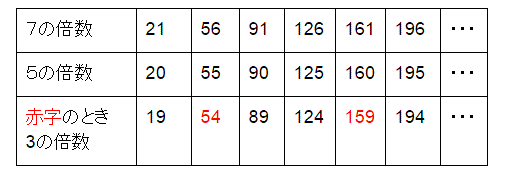
３段目の数Aについて。
54以降、35と３の最小公倍数である105を足すごとに３の倍数になるので、
54、159、264、369、474、579、684、789、894、999 ・・・
と続きます。
この中でAが３桁の整数となるのは９個です。
スポンサーリンク
