問題
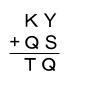
以下の各アルファベットには、それぞれ0~9のいずれかの整数が対応し、次の5桁の数からなる計算式を満たす。ただし、異なるアルファべットには異なる整数が対応し、同じアルファベットには同じ整数が対応するものとする。

このとき、次のアルファベットの関係式のうち正しいのはどれか。
- S=Y+1
- S=Y+2
- S=Y+3
- S=Y+4
- S=Y+5
2008 国家Ⅰ種
解答
解説
論理できっちり詰めきるのは難しいです。ある程度まで絞った後は、あてはめ(場合分け)で答えを探るのが実践的ともいえます。
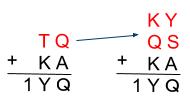
O(オー)と0(ゼロ)が紛らわしいので、O(オー)をQに変えます。
つまり
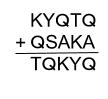
とします。
一の位より、Q+A=Q よりA=0
百の位を見ると、Q+A(0)=Kと値が変わっているので、十の位で繰り上がっていることがわかります。
よって、T+K=10+Y また百の位より、K=Q+1です。
ここまでは定石通りともいえる手順です。この後は、どこに着目するかで様々な解き方があります。前述したとおり、あてはめで答えを探ることが最良の手順ともいえます。
KとQの個数が多いので、そこから探れば結構すぐに求まります。
K=Q+1 と一万の位で繰り上がりがないことより、KとQの候補は以下の4組です。
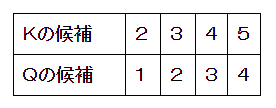
K=2 Q=1ならば
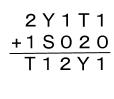
十の位のT+2 は繰り上がる必要あり、いずれにしろY=1か0になる。異なるアルファべットには異なる整数という条件に反するためこれは不適である。
以下同様にどんどん調べていくことが最短の解法と思います。
K=3 Q=2 と K=5 Q=4 もうまくいきません。
K=4 Q=3 のとき
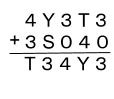
一万の位より、Tは7か8
T=7のとき(千の位で繰り上がりなし)
十の位より、Y=1
千の位より 、S=2 これが条件にあてはまっている。
T=8のとき(千の位で繰り上がりあり)
十の位より、Y=2
千の位は繰り上がりの必要があり、これを満たすSは存在しない。
よって、T=7、Y=1、S=2 であり S=Y+1 が求める答えである。
参考 論理でさらに絞っていく一例を以下に示します。
百の位では繰り上がっていません。もし繰り上がっていれば、Q=9となりますが、そのときK=0
これは成り立ちません(A=0で使用済み)。
百の位で繰り上がっていないため、一万の位と千の位に着目して
が成り立ちます。
これを十の位と一の位の足し算に代入します。
これにK=Q+1、A=0を代入して
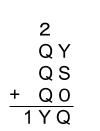
この式の、十の位に着目して、Q=3、4、5のいずれかです。
ただし、Q=5のとき、K=6となり、与式の一万の位の足し算が成り立たず不適です。
Q=3のとき、
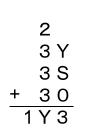
より、Y=1、S=2 となります。 よって、S=Y+1が答えです。
Q=4のとき、K=5
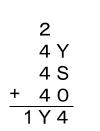
より、Y=4、S=0 これは不適(A=0で使用済み)
あるいは、Y=5、S=9 これは不適(K=5で使用済み)
スポンサーリンク
