問題
A、B、Cは1、2、3のいずれかの異なる数であり、ある整数を4進法で表すとABAC、8進法で表すとACCとなる。この数を10進法で表したとき、正しいものは次のうちどれか。
- 133
- 144
- 155
- 166
- 177
2003 市役所
解答と解説
解答
3
解説
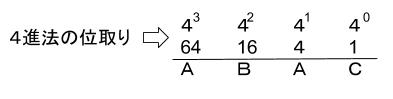
⇒ 選択肢を使いましょう。10進法で133~177となるので、A=2です。
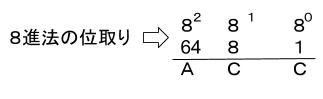
⇒ こちらも、選択肢から、A=2で間違いないことが確かめられます。
A=2が確定したので、それを入れると下のようになります。
4進法の表記から
⇒10進法で、64×2+16B+4×2+C・・・①
8進法の表記から
⇒10進法で、64×2+8C+C・・・②
①=②なので、
64×2+16B+4×2+C=64×2+8C+C
この式を整理して8で割ると
2B+1=C
この式を満たすB、Cを探します。
A、B、Cは1、2、3のいずれかの異なる数で、A=2なので、
B=1 C=3 か B=3 C=1 のどちらがこの等式を満たすかが求まればよいのです。
条件に合うのは、B=1 C=3 です。
よってこの数は8進法で233 であり、10進法で 64×2+8×3+3=155 です。
スポンサーリンク
