【和と差】問題５

解答

解説

大きい順にA、B、Cとすると
A+B＝79
A+C＝67
この２式の差より、B－C＝12　と決まります。
よって、A－B　と　A－C　の差も12となります。

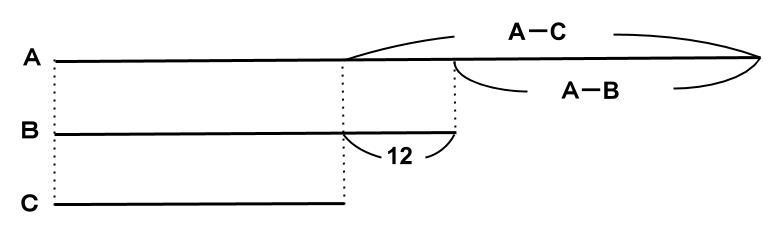
差が12となるのは21と33しかないので、
A－B＝21
A－C＝33　　と決まります。
以上より、A＝50、B＝29、C＝17　と求まります。
よって、A+2B+3C＝159　です。

※論理でがっちり攻めきれないときは、ある程度はあてはめで探したほうが速いです。
3番目に大きい46は　B+C　か　A－C　　でしょうから、最大でもこの２通りを調べれば求まります。

※B－C＝12　と偶数なので、B+Cも偶数。B+C＝36で鉄板でしょう。
非常にたくさんの解き方がある問題といえます。
与えられた６つの数をすべて足しても解けます。代数的な解法です。

解答

解説

ほぼ同じ問題が国家総合職でも近年出題されました。初出は2009年の算数オリンピックではないかと思います。

大きい順にA、B、C、Dとすると
A+B＝95
A+C＝85
よって、B－C＝10　なので　B＋Cは偶数となります。
B＋C＝48が最有力でしょう。　　※論理で詰め切るより、調べたほうが速いでしょう。

Ｂ＋Ｃ＝48ならば、
Ｂ－Ｃ＝10　と連立して

Ｂ＝29　、C=19

A+B=95　より
Ａ＝66

与えられた値の２は、Ｃ－Ｄ＝２　しかあり得ないので
Ｄ＝17

これで条件に合わない箇所がないかを調べると
Ａ＋Ｂ＝95
Ａ＋Ｃ＝85
Ａ＋Ｄ＝83
Ｂ＋Ｃ＝48
Ｂ＋Ｄ＝46　・・・これが答え
Ｃ＋Ｄ＝36
Ａ－Ｂ＝37
Ａ－Ｃ＝47
Ａ－Ｄ＝49
Ｂ－Ｃ＝10
Ｂ－Ｄ＝12
Ｃ－Ｄ＝２
矛盾がないことがわかります。
※矛盾があったら、他を調べます。