問題
長さが1cmのまっすぐな線をいくつか紙にかいて図形をつくります。紙から鉛筆をはなさずに、この図形上にある1点Aから、すべての線をなぞってAに戻ることを考えます。
12本の線でつくった下の図形には、そのうち4本の線を2回、他の線をちょうど1回ずつなぞってAに戻る、長さ16cmのなぞり方があります。このとき、2回なぞる4本の線の選び方は何通りあるか。
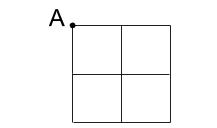
- 7通り
- 10通り
- 12通り
- 14通り
- 15通り
想定問題 出典 2019年筑波大学附属駒場中学
解答と解説
解答
1
解説
いわゆる一筆書きの問題です。
まずは、一筆書きの超有名法則の確認からです。
「すべて偶点の図形は一筆書きが可能」
「奇点がある場合は、奇点が2つの図形だけ一筆書きが可能。そのとき、奇点からスタートし、もう1つの奇点でゴールする」
偶点、奇点とは、ある点を通過する道の数による分類で、
道の数が偶数なら、偶点
道の数が奇数なら、奇点
これは超有名知識です。大丈夫でしょうか?
それでは、この知識ありきでこの問題に臨むわけです。
まず与えられた図形の頂点の偶奇を調べます。
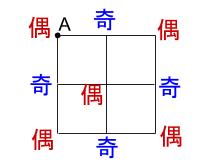
そして、2回なぞることが許されています。
つまり、下図における赤い道を2回なぞるとすれば、ここに2本の道があるのと同じことです。
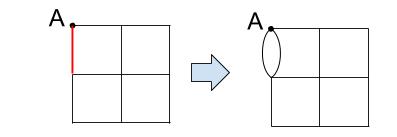
この図形の頂点の偶奇を調べます。
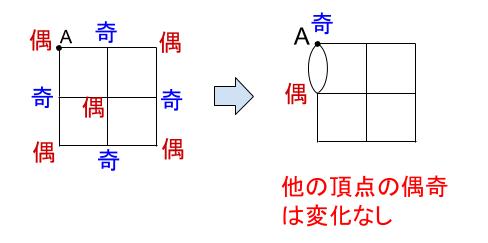
つまり、2回なぞる道の両端の頂点の偶奇が入れかわります。
よって、2回なぞる4本をうまく選んで、すべての頂点を偶点にすることが目標です。
そして、そのような4本の選び方は何通りあるのか?
このような問題なのです。
※点Aから点Aまでの一筆書きなので、奇点はなし
ここから先は、ていねいに場合分けをして調べていきます。
2回なぞる道を赤い道とすると、以下のようになります。
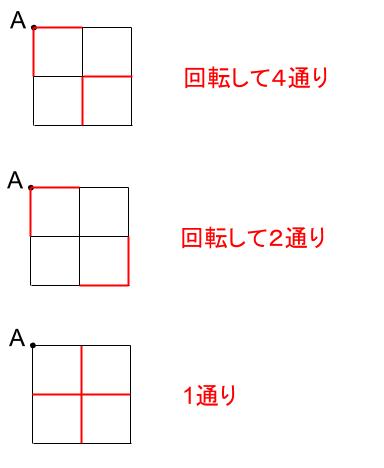
よって、4+2+1=7
より、7通りです。
スポンサーリンク
