問題
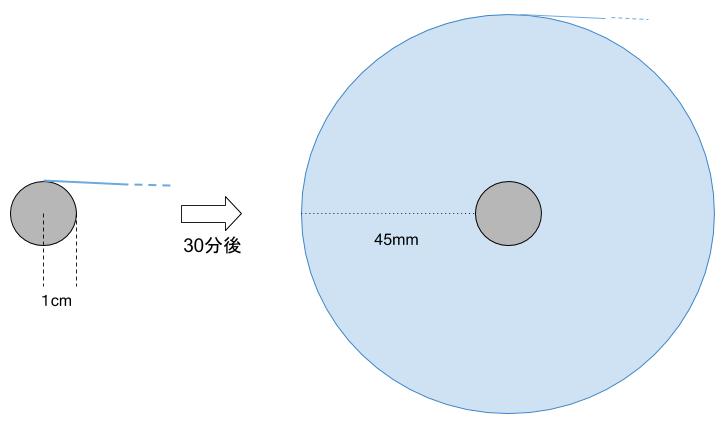
毎秒1回転する半径1cm の芯に、厚みが均一のテープをたるまないように巻き付けたところ、巻き付け始めてからちょうど30分でテープ部分の厚みは45mmになった。このとき、芯に巻き付けられたテープの長さはおよそ何mか。
- 207m
- 287m
- 367m
- 447m
- 527m
国家総合職 2012
解答と解説
解答
3
解説
新傾向と分類されかねない本問も、中学受験の世界では古典中の古典。おそらく25年くらい前に麻布中学校で初出です。
すっきりとした解き方が確立されています。
テープを横(図の方向)から見たときの面積を考察します。
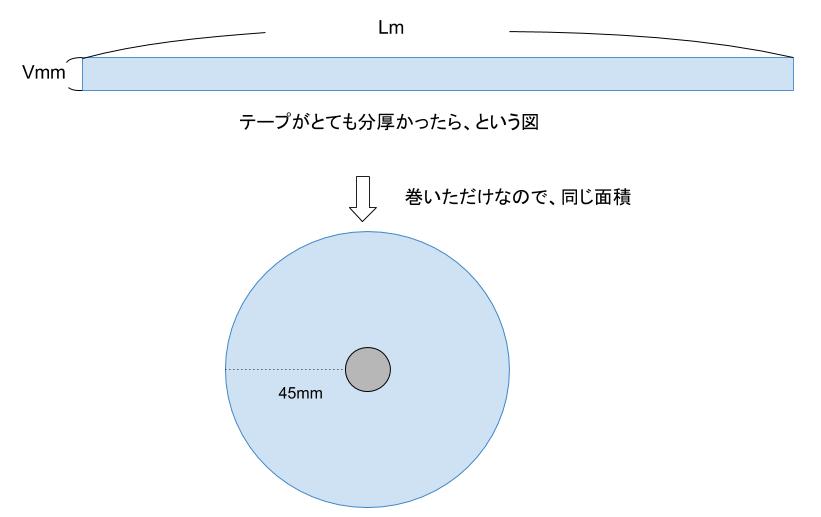
求める長さをLm=L×1000mm、テープの厚みをVmmとします。
Vは巻かれたテープの厚み45mmを、テープを巻き付けた回数で割ったものになります。
30分=1800秒なので、1800回巻き付けています。
よって、V=45/1800=1/40 (mm)です。
テープを一直線に伸ばしたとき、テープを横から見たときの形は長方形で、その面積をSとすると、
S=V×L×1000
なので、
S=25×L (mm2) ・・・①
テープを図のように巻いたとき、テープを横から見たときの形は大円(半径55mm)から小円(半径10mm)を引いたもので、その面積は
(55×55-10×10)×π (mm2)・・・②
①=② なので、
25×L =(55×55-10×10)×π
π=3.14で近似計算をすると、
L=367.38(m)
これは約367mで、答えは3です。
スポンサーリンク
